DIY pseudorandom number generator

This post explores how to create a pseudorandom number generator based on the logistic map.

Background

Veritasium has a great video about the logistic map, particularly how it can demonstrate chaotic behavior. If you haven’t seen his video before, I highly recommend you check it out.

Anyways, this relatively simple equation known as the logistic map looks like this:

$$x_{n+1}=rx_n(1-x_n)$$

For certain values of $r$, the values of $x$ follow a predictable pattern, but for other values of $r$, such as when $r=4$, the values of $x$ become unpredictable and chaotic.

Through this unpredictable behavior, the logistic map provides a promising approach to pseudorandom number generation as discussed in the paper Logistic map: A possible random-number generator .

As suggested from this paper, the following mapping can be applied to all $x$ values such that they provide a uniform distribution:

$$y_n = {\frac 1 \pi} \arccos (1 - 2x_n)$$

Simple Implementation

Implementing the couple of equations in our previous section is pretty straight forward as shown in the following Python class.

class RandomNumber:
    r: Final[int] = 4

    def __init__(self, seed: float = 1 / 3) -> None:
        self.x = seed

    @staticmethod
    def map_to_uniform(x: float) -> float:
        return math.acos(1 - 2 * x) / math.pi

    @staticmethod
    def calc_logistic_map(r: int, x: float) -> float:
        return r * x * (1 - x)

    def __call__(self) -> float:
        self.x = self.calc_logistic_map(self.r, self.x)
        return self.map_to_uniform(self.x)

Using this class, we can easily sample a bunch of uniformly distributed random variables.

rand = RandomNumber()
rands = [rand() for _ in range(1000000)]

Now let’s visualize these samples on a histogram:

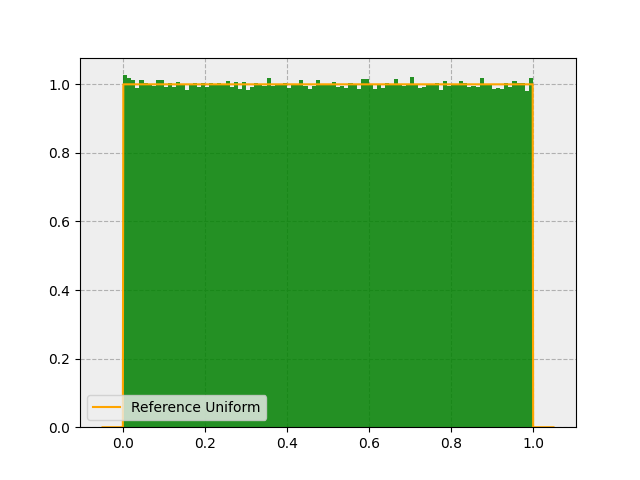
Looks great! What does the distribution look like if we sum the value of 2 random variables? I.e.

$$\textit{X} = \mathcal{U}_0 + \mathcal{U}_1$$

Or in Python:

rand = RandomNumber()
rands = [sum(rand() for _ in range(2)) for _ in range(100000)]

Gives us this:

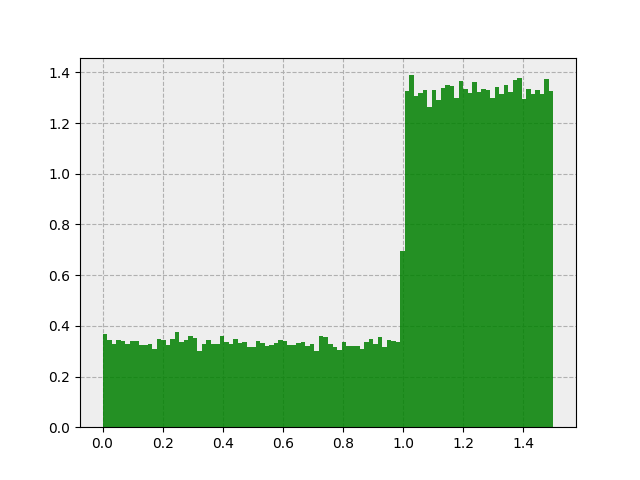
Oh no! What’s going on? The sum of 2 uniformly distributed random variables should give us a triangular-looking distribution, not this.

As it turns out, consecutive samples from our pseudorandom number generator are correlated with one another. In the next section we’ll address this issue.

Better Implementation

Here is an improved implementation of our pseudorandom number generator which drops intermediate values to reduce correlation between consecutive samples.

class RandomNumber:
    """@article{phatak1995logistic,
    title={Logistic map: A possible random-number generator},
    author={Phatak, SC and Rao, S Suresh},
    journal={Physical review E},
    volume={51},
    number={4},
    pages={3670},
    year={1995},
    publisher={APS}}"""

    r: Final[int] = 4

    # The random numbers generated from this class should be uniformly distributed between 0 and 1
    upper_limit: Final[float] = 1
    lower_limit: Final[float] = 0
    theoretical_mean: Final[float] = (upper_limit + lower_limit) / 2
    theoretical_variance: Final[float] = (upper_limit - lower_limit) ** 2 / 12

    def __init__(self, seed: float = 1 / 3, skip: int = 22) -> None:
        if skip < 0:
            raise ValueError(f"'{skip}' is not an acceptable value for 'skip'. 'skip' must be >= 0.")
        self.x = seed
        # NOTE: A skip of at least 1 is necessary to remove obvious sample-to-sample correlation,
        # but a skip of around 22 removes all single precision correlation (see referenced paper).
        self.skip = skip

    @staticmethod
    def map_to_uniform(x: float) -> float:
        return math.acos(1 - 2 * x) / math.pi

    @staticmethod
    def calc_logistic_map(r: int, x: float) -> float:
        return r * x * (1 - x)

    def __call__(self) -> float:
        for _ in range(self.skip + 1):
            self.x = self.calc_logistic_map(self.r, self.x)
        return self.map_to_uniform(self.x)

With this new implementation, the following code:

rand = RandomNumber()
rands = [sum(rand() for _ in range(2)) for _ in range(100000)]

Gives us this:

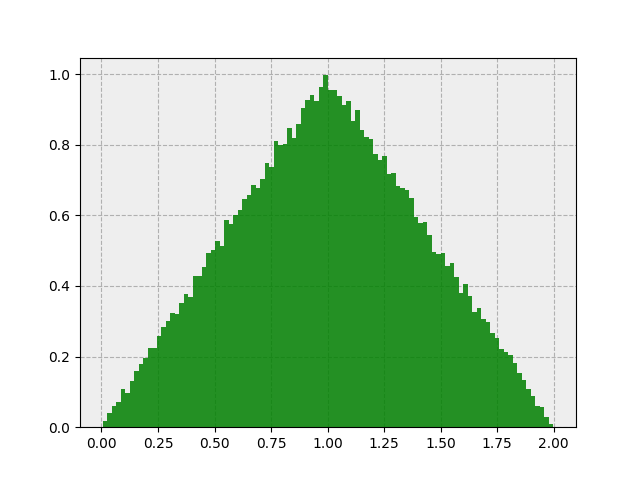
Excellent! Also, under the central limit theorem, the sum of 100 uniformly distributed random variables should be approximately Gaussian. I.e.:

$$\mathcal{N}_{\mu,\,\sigma^2} \approx \sum_{i=0}^{99} \mathcal{U}_i$$

This can be expressed in the following Python class:

class PseudoGaussian:
    def __init__(self, N: int = 100) -> None:
        self.N = N
        self.rand = RandomNumber()

    def __call__(self) -> float:
        return sum(self.rand() for _ in range(self.N))

    @property
    def theoretical_mean(self):
        return self.N * self.rand.theoretical_mean

    @property
    def theoretical_variance(self):
        return self.N * self.rand.theoretical_variance

And running this short snippet:

rand = PseudoGaussian(N=100)
rands = [rand() for _ in range(100000)]

Gives us this:

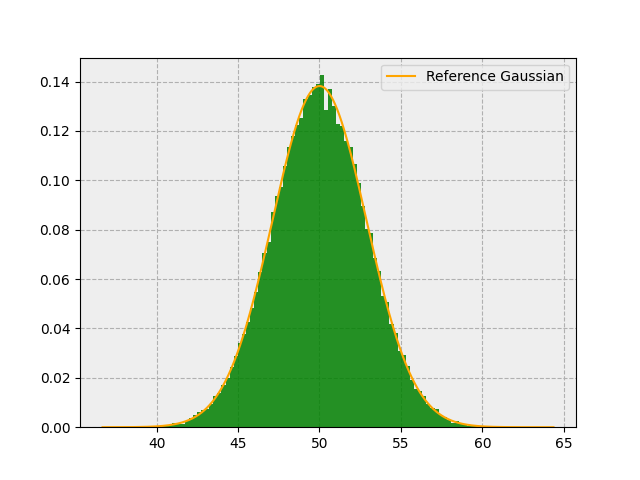
Sure enough, our output distribution looks very Gaussian!

I hope you’ve enjoyed this post. If you have any feedback, please feel free to reach out.

Also, you may be interested in this post where I use the pseudorandom number generator in a Metropolis-Hastings implementation.

Published on 25 February 2022

If you enjoy this blog, please consider supporting me by buying one of my books. 📚
(click here)